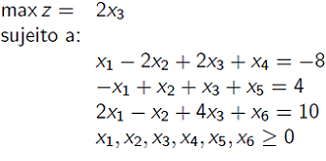Introdução
A Programação Linear (PL) tem sido uma importante ferramenta de análise para grandes empresas pelo mundo. Em um breve resumo, ela se propôe a otimizar recursos limitados para atividades que competem entre si.
A Programação Linear utiliza de um modelo matemático para descrever o problema proposto. Através desse modelo proposto, é feita uma análise gráfica, mostrando qual será a região de soluções viáveis. Segue-se abaixo um exemplo da região com as retas de restriçoes de um problema:
Exemplo:
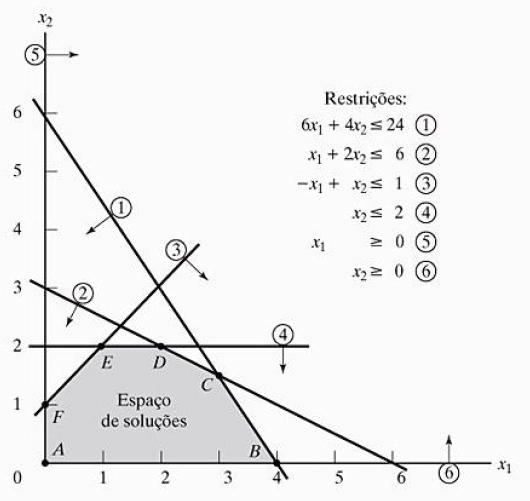
A determinação da solução ótima requer identificar a direção na qual a função objetivo z aumenta (maximização) ou diminue (minimização). O ponto dentro da região viável onde z é maior (maximização) ou menor (minimização) será a solução ótima.
Segue-se abaixo um exemplo:
Exemplo:
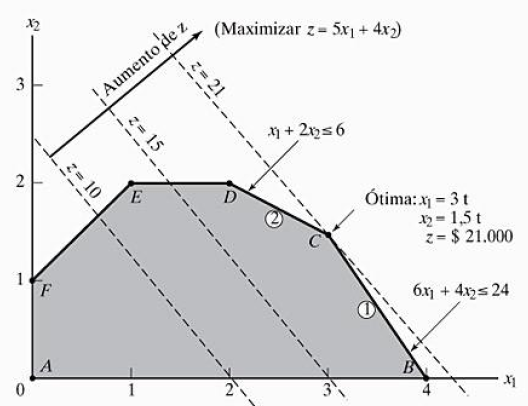
Solução:
A solução ótima se encontra no ponto C.
Resolvendo PL Usando método Simplex
O método Simplex não enumera todas as soluções básicas (pontos extremos), porém ele analisa algumas dessas soluções selecionadas.
Abaixo é representado um modelo de PL com a região de soluções viável.
Modelo de PL:

Região de Soluções viável:
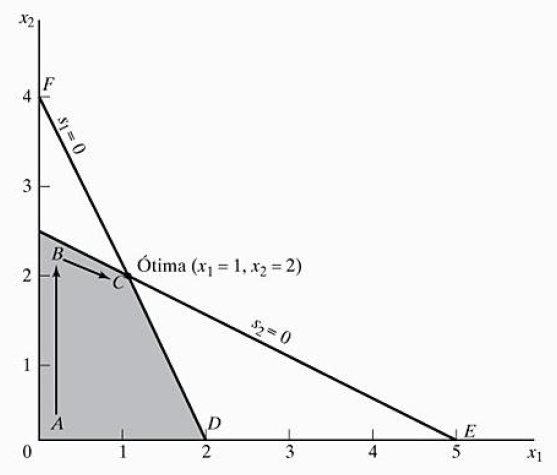
O método iterativo normalmente inicia no ponto de origem A. Logo após, é analisada se a utilização de um ponto com x1 ou x2 maior que 0 poderia melhorar a função objetivo z. Analisando a função objetivo podemos afirmar que sim.
O projeto Simplex exige que se melhore apenas uma variável por vez, analisando qual delas traria uma maior taxa de melhora para a função objetivo. Para o exemplo citado, o valor da função objetivo aumentará em 2 para cada unidade de x1 e 3 para cada unidade de x2. Portanto, a variável escolhida seria x2. A figura mostra que x2 será aumentado até alcançar o ponto extremo B.
Logo após, o valor de x1 será aumentado até alcançar o ponto C que é o ótimo. Portanto, o método percorre um caminho pelas bordas, até atingir um valor ótimo.
Segue-se abaixo uma estrutura de representação para o método:
Estrutura do Simplex:

Método Simplex de Grande-M
De acordo com o problema de PL, se houverem restrições do problema que demandem variáveis artificiais, elas são adicionadaspara formar uma solução inicial semelhante é solução básica em que todas as variáveis são de folga. Contudo, como essas variáveis não fazem parte do modelo original, elas recebem punições muito alta na função objetivo, forçando-as a ter o valor 0 na solução ótima.
Portanto, para o problema abaixo, é inserida variáveis artificiais para as 2 primeiras equações, e elas são inseridas com suas punições na função objetivo (a soma delas é pelo fato do problema ser de minimização).
O valor de M a ser usado depende do problema, ele deve ser suficientemente grande em relação aos coeficientes da função objetivo original.
Modelo de PL:

Método Grande-M
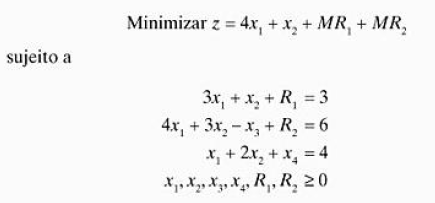
Método Simplex de Duas Fases
No método do Simplex Grande-M, as punições M devem ser grandes em relação aos coeficientes da função objetivo, resultando assim em erros significativos de arredondamento. O método do Simplex Duas Fases elimina essa constante M.
O método Duas Fases como o nome já diz, resolve o problema em duas fases:
- Fase I: Tenta achar uma solução básica inicial, e se ela for encontrada passa para a Fase II.
- Fase II: É invocada para resolver o problema original.
Como um resumo de atuação do método, temos:
Resumo do Método das Duas Fases

Método Simplex Generalizado
O Simplex generalizado é utilizado quando a solução básica inicial é não factível e não ótima. As restrições do modelo devem ser somente da relação menor igual.
Este método combina o simplex primal com o simplex dual. Portanto, quando a solução é infactível, usa-se as regras do simplex dual até reestabelecer a viabilidade ou certificar que não existe solução factível. Quando a solução é factível, usa-se as regras do simplex primal.
Um facilitador no uso do Simplex generalizado, é que não existe a necessidade de uso de variáveis artificiais.
Modelo de PL:
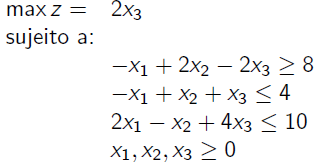
Apenas restrições menor igual
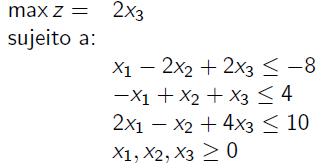
Inserção de variáveis de folga